
所長ー!今日のテーマはなんですか?

今日はとても神秘的な一般均衡理論の動学を見てみよう。動学的一般モデルは近年非常に発展してきており、そのカオス性など興味深い研究結果も出てきているテーマなんだ。
動学的一般均衡モデルの概要
まず、動学的一般均衡モデルについての定義を見ておこう。
動学的一般均衡モデル:通常の一般均衡モデルに時間的要素を導入したモデル
この応用例としては、マクロ経済学、国際経済学、財政学など様々である。
経済学においては均衡の安定性という概念が非常に重要視されているので、この動学理論においても当初は安定性が注目されていた。しかし、研究を通じて実際には均衡が安定的な場合だけでなく、カオス的に変動する場合も存在していることがわかってきている。
動学モデルと社会厚生関数
通常、動学的経済モデルでは、将来に向かって無限に時間が続くと仮定する。これを\(t=0,1,2,…\)とし、\(t=0\)を現時点として、時点\(t-1\)と\(t\)の間の期間を期間\(t\)とよぶ。
消費者は(a)将来の効用を割り引いて考える(または(b)無限に生き続ける訳ではなく、各世代は一定期間しか生きないが利他的であると仮定する。)すると、現在から未来まで(または自分の一生と子の世代)を含めて消費者が感じる効用の総和を効用和$U$とする。それをもとに社会全体の厚生を考える。各個人の効用にパラメータ$\theta_i$をかけて評価し、足し合わセて社会厚生和を以下のように考えてみる。
$$U=\theta_\alpha U_\alpha + \theta_\beta U_\beta$$
これを根岸の社会厚生関数と呼び、競争均衡においてはこれが最大化されていることが知られている。$\theta$は消費者ごとの効用和の帰属価値と呼ぶ。
競争均衡配分は社会厚生関数を最大化している
均衡動学系
あるパラメーターがどのように時間に応じて動いているかを経路という。ここからは、資本が競争均衡においてどのように動くか、という競争均衡経路を、均衡動学系というシステムで動きを記述することを考える。この動学系(または力学系)とはある時点の状態を一時点前の状態で記述するシステムのことである。
競争均衡経路においては、ある前期の資本$k_{t-1}$のもとで、当期の社会厚生関数と来期以降の社会厚生関数の割引現在価値の合計を最大にするような今期の資本$k$が定まっているはずである。そのような均衡経路上の資本の動きを、$h$を用いて以下のように記載する。
$$k_t = h(k_{t-1} ; \theta)$$
このシステムを均衡動学系という。
動学系:ある時点の状態を一時点前の状態で記述するシステム
均衡動学系:均衡状態におけるパラメータ(資本)がどのように時間と共に動くかを記述したシステム
競争均衡経路上の安定性
競争均衡経路上の配分は、時間と共に変化するものだが、時間が経っても変化しない時、経済は長期均衡にある、という。
この長期均衡は競争動学系の不動点となる。不動点とは、
$$k^s = h(k^s ; \theta)$$
となる点$k^s$を指す。
このような不動点に資本のレベルが収束することを大域的に安定であるといい、その条件は将来の効用の割引因子$\rho$が十分に1に近いことであることが証明されている。
命題2
与えられた生産関数$c$や効用関数$u_i$のもとでは、将来の効用の割引因子$\rho$が十分に1に近い時には、長期均衡は大域的に安定である。
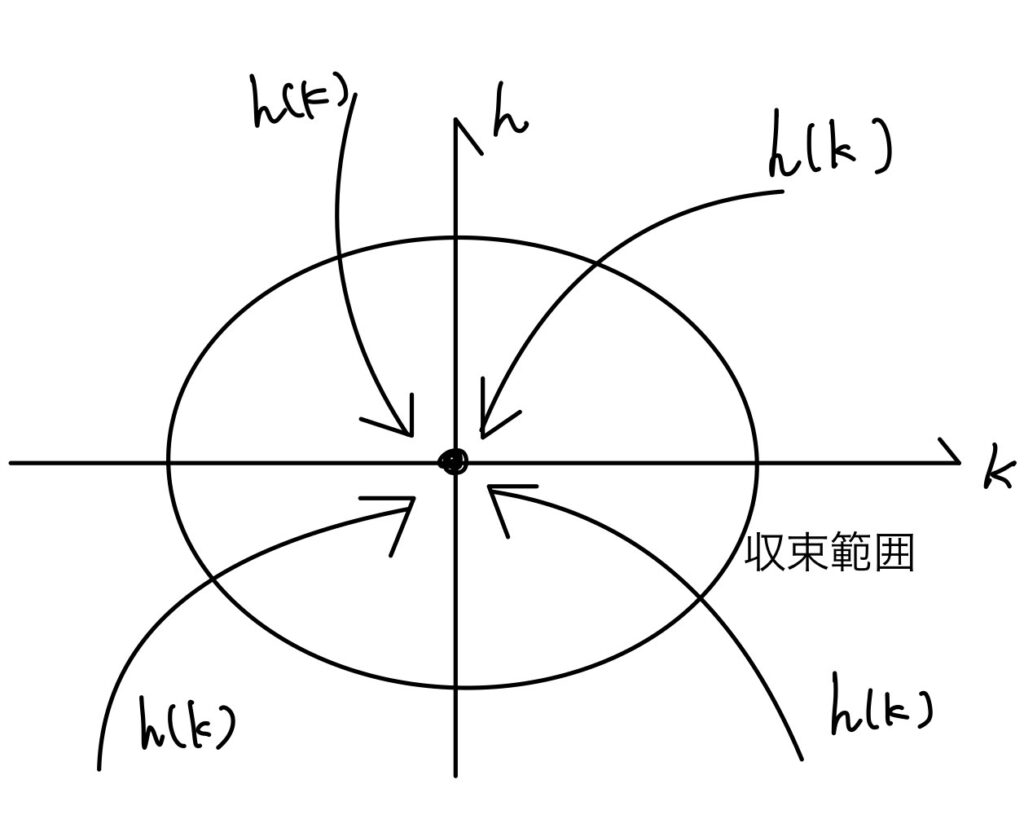
図1 均衡動学システムhがある収束範囲に大域的に安定する様子
カオス的景気変動とは
矢野によれば、長い間、動学分析においても長期均衡や局所的安定性と言った安定性の研究ばかりが盛んであったといい、それは単に伝統的な経済学の長期安定性への思い入れによるところであったとしている。しかし、1950年代以降はコンピューターによる非線形な動学系の分析によって、それがこれまで考えてきた単純な線形関数とは全く異なる性質を持つことや、カオスと呼ばれる不規則な運動を示すことがわかってきた。
均衡動学系$h(=k_t)$と、前期の資本$k_{t-1}$の間の関係を、競争均衡における消費者の帰属ベクトル$\theta$をパラメータとし、曲線Hとしてグラフに描いてみる。
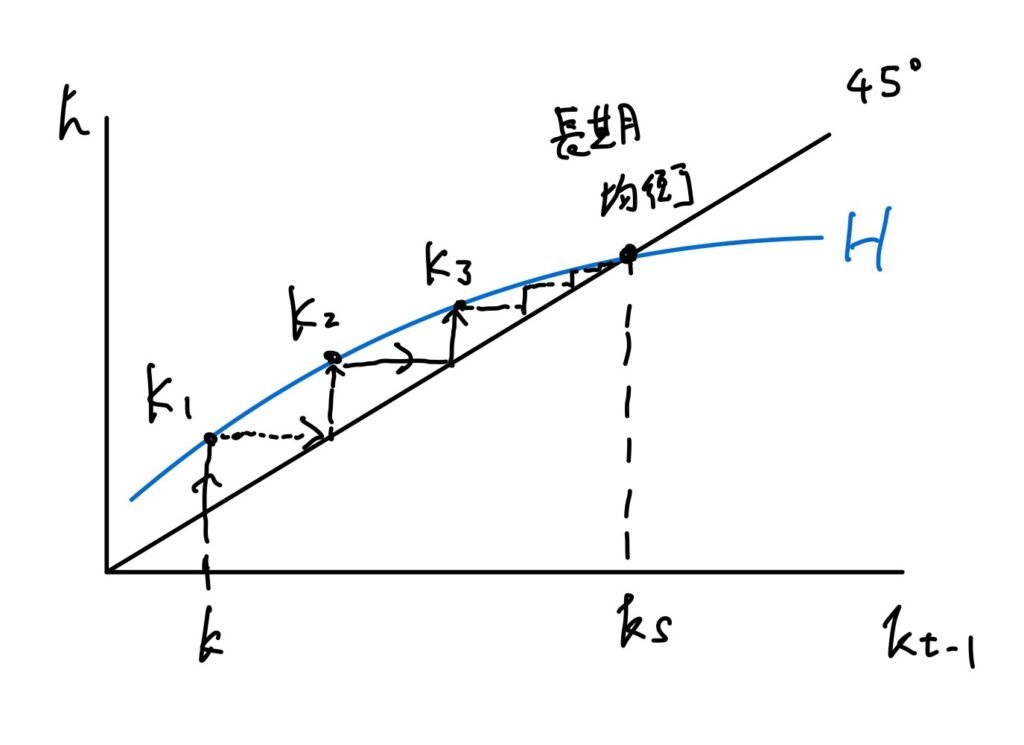
図2 動学経路と長期均衡
この曲線Hは、先ほどの動学的競争均衡における資本経路となっている。今、資本kが初期条件として与えられると、それに対応して$k_1 = h(k, \theta)$として、点$K_1$にて第1期の資本が決定される。第2期の資本をみるためには、45度線をグラフに書き入れる。点$K_1$から横軸と並行に矢印を伸ばし、45度線にぶつかるところで座標を取れば、その点のk座標が第1期の$h$の値になるので、そこから曲線Hへと縦に並行に矢印を伸ばせば、次の点$K_2$にて第2期の資本が決定される。同様にして、第3期、第4期と競争均衡経路における資本量を辿ることができる。
非線形な均衡動学について
経済学において、最近の研究によって均衡動学系に強い非線形を与える力が働く可能性が明らかにされており、非線形な均衡動学を考えることは重要である。動学系が非線形の場合、線形動学系では記述できない多くの現象が認められる。図4が示すようにあるkから出発すると、非線形の場合には周期的に循環する動きとなることがある。
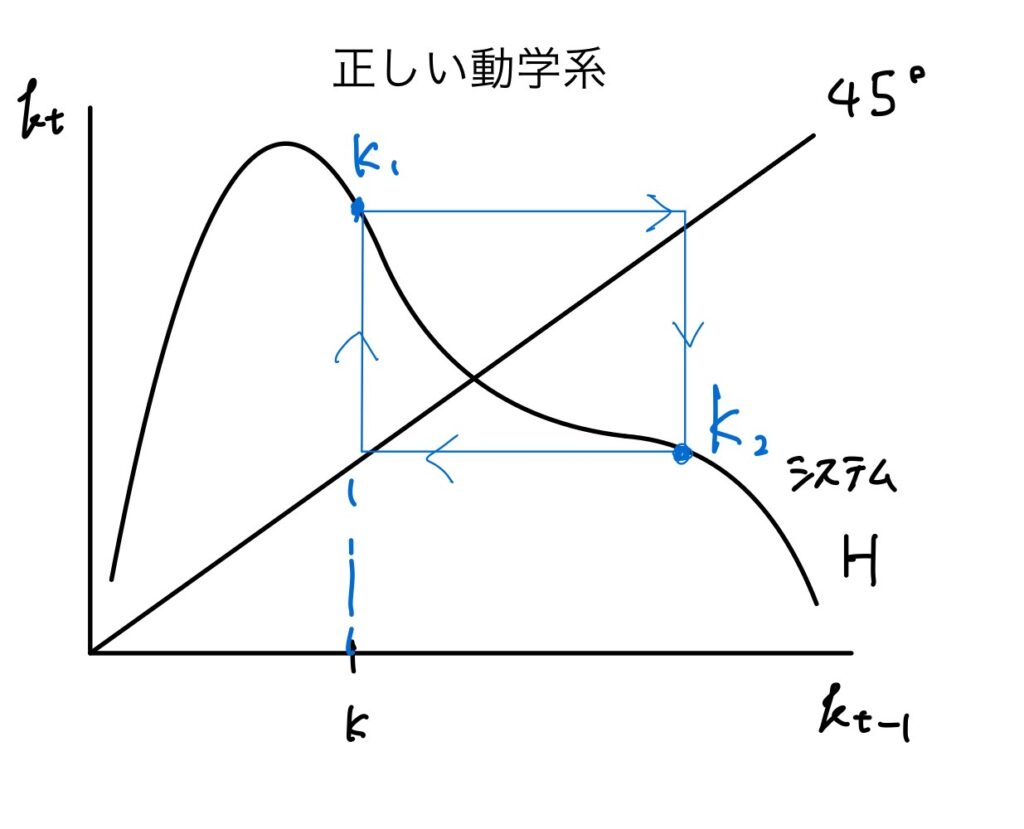
図3 非線形な動学系
非線形な動学系を線形近似で表そうと思っても、元の動学系と線形近似動学系では、性格が異なってしまうことがある。図4のように近似動学系では$k_s$に収束してしまう。
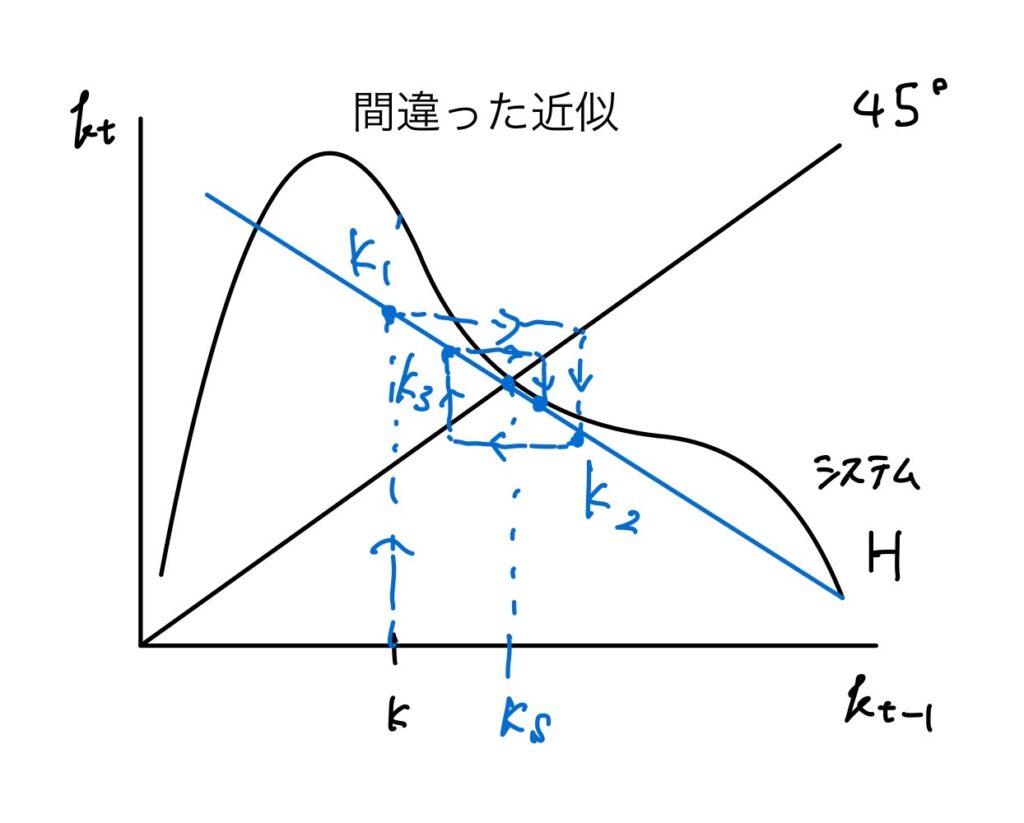
図4 近似した動学系
非線形動学系による重要な現象がカオスである。
カオスは、非常に不規則で、確率的に動いているように見えるが確率的要因を全く含まない動学系を指す。カオスの性質としては、似たような初期条件でもシステムの最終的な結果が大きく異なるという初期条件への鋭敏性、ある一定の集合の中で系が動くという有界性などの性質を持っている。また、初期条件への鋭敏性から未来のある時点における厳密な結果を算出することが難しいため、確立分布をもとにその結果の期待値を算出するという手法をとることが多い。
カオス:確率的に動いているように見えるが確率的要因を全く含まない動学系
競争均衡経路が振動するケース
さて、競争均衡経路Hの分析に戻ると、ある条件において、図5のように均衡経路は長期均衡の周りで振動をする。
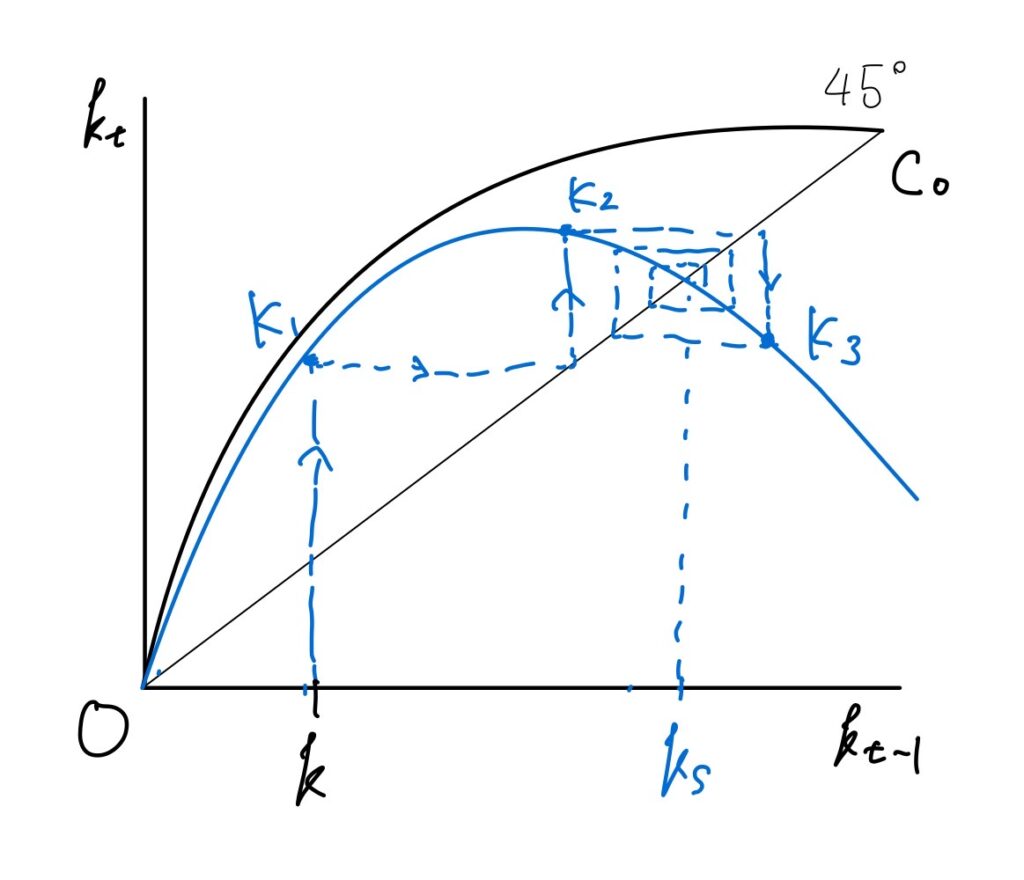
図5 振動する場合
また、動学系の形によっては、1点に収束せず、長期均衡が周期2の循環経路となる場合もある。この場合、資本が増えたり減ったりという循環をすることが最適となるのだ!
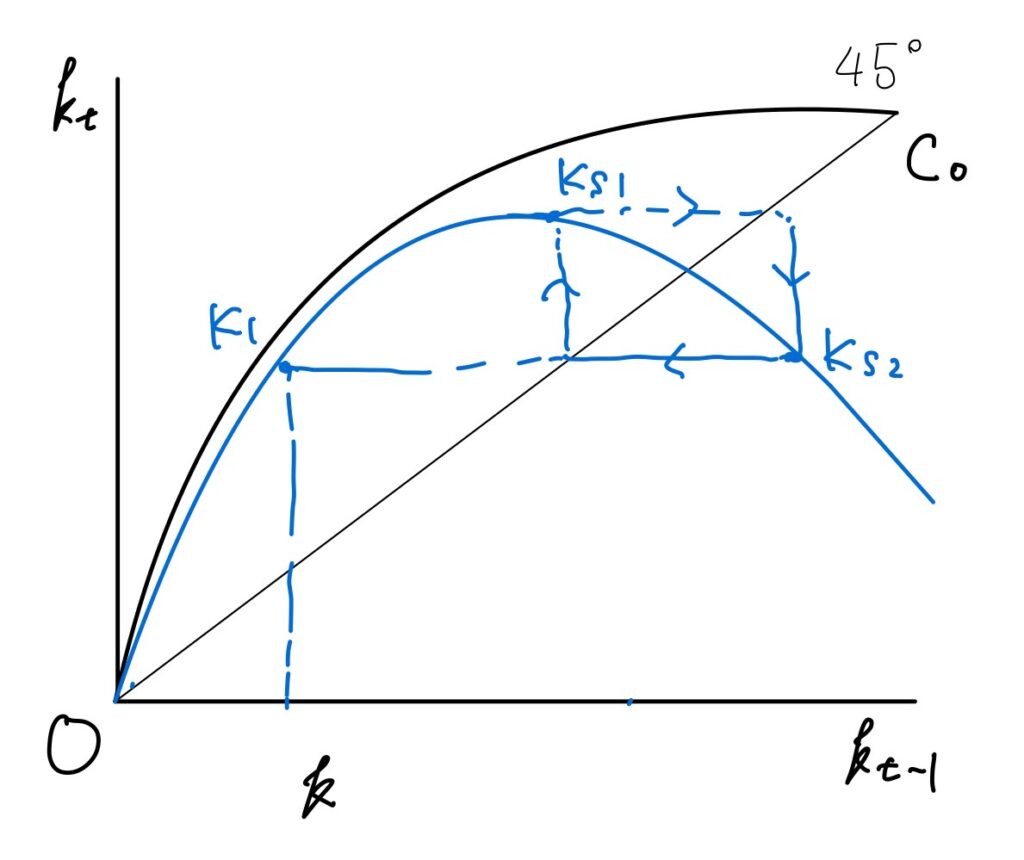
図6 循環する場合
均衡が振動する条件について
これはどのような場合に起こるのか?この点については研究(下記参考文献)において触れられていなかったので考察すると、それは資本の成長期において、同じ資本生産量の場合に前期に比べて感じる効用が多くなる場合であると考えられる。
これについては、技術発展や学習効果によって同じ資本財の量でも、そこから得られる消費財による効用が増えることは考えられる。同じ資本の量だとしても(ここでの資本は貨幣ではない)技術的に可能な範囲はイノベーションによって拡大し続けているので、それが資本の増加スピードが早い頃に起これば実現する。
均衡が一点に安定しないというはとても面白い現象で、大学レベルの経済学で教えられたこととは大きく異なるものの、不確定な実社会にフィットしているような安心感もある。ただし、カオスといえど、完全にどこにいくかがわからないわけではない。むしろ、長期均衡を中心とした一定の範囲内に長期的には収束する傾向にある。また、ショックが起こり、一時的に均衡から離れたとしても、また時間をかけて戻っていくことができるという安定性を持っている。

このような性質は景気の変動の分析などに使われており、非常に有用なんだよ!
参考文献
今回の内容はこちらの「現代の経済理論」の六章「一般均衡理論の動学的展開」(矢野誠)が出典です!岩井克人先生や神取先生ら東大のトップ陣が著者に入っており、根岸先生の業績を交えつつも、妥協しない深い解説がされた邦書という珍しい本です。
今回取り上げた内容以外にも、岩井克人先生や神取先生の解説パートなどはわかりやすく、かつ実際の研究も取り上げてゲーム理論、経済成長論の発展の歴史と研究過程の難しさを解説しており、おすすめです。ぜひ読んでみてください。


コメントを残す コメントをキャンセル